니콜로 타르탈리아
"오늘의AI위키"의 AI를 통해 더욱 풍부하고 폭넓은 지식 경험을 누리세요.
1. 개요
니콜로 타르탈리아는 16세기 이탈리아의 수학자, 공학자, 그리고 번역가였다. 그는 3차 방정식의 해법을 발견했지만, 지롤라모 카르다노가 이 해법을 자신의 저서에 발표하여 '카르다노의 공식'으로 알려지게 되었다. 타르탈리아는 또한 파스칼의 삼각형(타르탈리아의 삼각형)을 발견하고 이항 정리에 능숙했으며, 유클리드의 '원론'과 아르키메데스의 저술을 번역하여 수학 발전에 기여했다. 그는 탄도학 연구에도 선구적인 업적을 남겼으며, 군사 과학 분야의 저술은 유럽 전역에 큰 영향을 미쳤다. 타르탈리아는 1557년 베네치아에서 사망했다.
니콜로 타르탈리아는 1500년경 이탈리아 브레시아의 가난한 집안에서 태어났다. 본명은 니콜라 폰타나(Nicola Fontana)이다. 어린 시절 프랑스 군의 침입으로 아버지를 잃고, 자신도 턱에 큰 부상을 입어 말더듬이가 되었다. 이 때문에 '타르탈리아(말더듬이)'라는 별명을 얻었다.[2] 어려운 환경 속에서도 독학으로 수학을 공부한 그는 3차 방정식의 해법을 발견하여 명성을 얻었다.
카르다노는 1539년에 3차방정식의 해법을 공개하지 않겠다는 약속을 받고 타르탈리아에게 그 해법을 전수받았다.[22] 타르탈리아는 세 가지 형태의 3차 방정식 해법의 비밀을 시로 공개했다.[22] 그러나 카르다노는 이후 스치피오네 델 페로가 타르탈리아보다 먼저 3차 방정식의 해법을 발견했다는 사실을 알게 되었다.[23] (타르탈리아는 이전에 델 페로의 제자 피오레에게 도전을 받았는데, 이를 통해 타르탈리아는 해법이 존재한다는 것을 알게 되었다.)[23]
타르탈리아는 네 꼭짓점 사이의 거리를 이용하여 삼각뿔(사면체)의 부피를 나타내는 공식을 고안했다. 이 공식은 헤론의 공식을 3차원으로 일반화한 것이다.
타르탈리아는 파스칼의 삼각형으로도 알려진 이항 계수를 구하는 삼각형 배열을 파스칼보다 100년이나 앞서 발견했다.[21] 이 삼각형은 오늘날 "타르탈리아의 삼각형"으로도 불린다.
다음 문제는 “타르탈리아의 문제”라고 불린다.[27] 어떤 상인이 목장을 지났다. 상인은 문지기에게, 여기 양은 몇 마리냐고 물었다. 그러자 문지기는 “두 마리씩 세어도, 세 마리씩 세어도, 네 마리씩 세어도, 다섯 마리씩 세어도, 여섯 마리씩 세어도 한 마리씩 남지만, 일곱 마리씩 세면 딱 맞다”라고 대답했다. 양은 몇 마리일까?
2. 생애 및 업적
1535년 안토니오 마리아 피올과의 수학 공개 논쟁에서 3차 방정식 30문제를 모두 풀어 승리했다. 이후 지롤라모 카르다노에게 3차 방정식의 해법을 알려주었으나, 카르다노가 이를 자신의 저서에 발표하면서 "카르다노-타르탈리아 공식"으로 알려지게 되었다.
1537년에는 탄도학 연구 성과를 담은 『노바 시엔티아(Nova scientia)』를 발표하여 근대 탄도학의 기초를 마련했다. 그는 포탄의 최대 사거리를 얻기 위해서는 포를 수평선과 45° 각도로 발사해야 한다는 것을 발견했다.[9]
1543년에는 유클리드 원론을 이탈리아어로 번역하여 출판했다. 이는 유클리드의 ''원론''이 현대 유럽 언어로 번역된 첫 사례였다.[14]
2. 1. 어린 시절과 교육
니콜로 타르탈리아의 본명은 니콜라 폰타나(Nicola Fontana)이다. 그는 브레시아 출신으로, 어린 시절 프랑스 군대의 침입으로 아버지를 잃었다. 1512년 캄브레 동맹 전쟁 중 루이 12세가 이끄는 프랑스군이 브레시아를 침공했을 때, 4만 5천 명이 넘는 주민들이 학살당했다. 이때 타르탈리아는 가족과 함께 대성당으로 피신했지만, 프랑스 병사에게 턱과 혀에 칼을 맞아 큰 부상을 입었다. 이로 인해 그는 말을 더듬게 되었고, '타르탈리아(말더듬이)'라는 별명을 얻게 되었다.[2] 그는 이후 수염을 길러 상처를 가렸다.
타르탈리아는 가난 때문에 정규 교육을 거의 받지 못했다. 그의 전기 작가 아르놀도 마소티에 따르면, 타르탈리아는 약 14세 무렵 프란체스코라는 선생님에게 알파벳을 배우러 갔지만, 'k'까지 배운 후 수업료를 낼 수 없어 그만두어야 했다.[3] 그는 "그날부터 저는 다시는 가정교사에게 돌아가지 않았고, 가난의 딸이라고 불리는 근면함만을 동반한 고인들의 작품에 대해 스스로 노력했습니다."라고 회고했다.[3] 그는 묘비에 새겨진 글자를 보며 글을 깨우쳤다는 일화가 있을 정도로, 사실상 독학으로 학문을 익혔다.
타르탈리아는 1517년경 베로나로 이주했고, 1534년에는 베네치아로 이주하여 산판학교에서 실용 수학을 가르치며 생계를 유지했다. 그는 수학 문제를 풀어주고 돈을 벌기도 했으며, 유클리드에 대한 강의 대가로 해진 망토를 받는 등 어려운 생활을 했다.[6]
2. 2. 수학적 업적
카르다노와의 갈등으로 유명하다. 1535년경 삼차 방정식의 해법을 발견하였으나 발표하지 않고 있다가, 카르다노의 요청으로 3차 방정식의 해법을 다른 사람들에게 가르쳐주지 않는 조건으로 알려줬다. 하지만 카르다노가 저서 《아르스 마그나》(Ars Magna)에 3차방정식의 해법을 실어 이후 "3차방정식의 해법"은 "카르다노의 공식"으로 불렸다.[2]
1535년, 삼차 방정식 수학 시합으로 유명해진 타르탈리아에게는 해법을 가르쳐 달라는 사람들이 쇄도했다. 카르다노는 출판하지 않는다는 조건으로 타르탈리아의 삼차 방정식 해법을 전수받았다. 수년 후, 카르다노는 제자 루도비코 페라리와 함께 독자적으로 타르탈리아와 같은 해법에 도달한 스치피오네 델 페로의 미발표 논문을 보게 되었다. 그 미발표 논문은 타르탈리아의 논문보다 앞서 작성되었기에, 카르다노는 약속은 무효라고 판단하고 1545년 뉘른베르크에서 발표된 저서 《아르스 마그나》에 실었다. 카르다노가 자신의 이름으로 해법을 발표한 것을 알게 된 타르탈리아는 격분했다.[2]
페로와 타르탈리아의 발견임을 명기한 상태에서의 발표였지만, 타르탈리아의 분노는 사그라지지 않았고, 타르탈리아는 수학 공개 시합을 신청했다. 그러나 카르다노는 이를 받아들이지 않고, 대신 제자 페라리와 시합을 하게 되었다. 승패에 대해서는 여러 설이 있으며, 페라리가 대승했다는 설이나 페라리의 지각으로 무효 경기가 되었다는 설 등이 있다. 현재, 삼차 방정식의 해법은 "카르다노의 공식"이라고 불린다.[2]
타르탈리아의 걸작은 베네치아 방언으로 쓰인 6부분으로 구성된 1500페이지 분량의 백과사전인 ''General Trattato di Numeri et Misure'' (''수와 측정에 관한 일반 논문'')이다.[15] 처음 세 부분은 타르탈리아가 사망할 무렵인 1556년에 출판되었고, 나머지 세 부분은 그의 문학 집행자이자 출판사인 쿠르시오 트로이아노(Curtio Troiano)에 의해 1560년에 사후 출판되었다. 데이비드 유진 스미스(David Eugene Smith)는 ''General Trattato''에 대해 "그 시대 이탈리아에서 출판된 최고의 산술 논문"이라고 평가했다.[16]
제1부는 554페이지 분량으로 상업 산술을 다루며, 당시의 복잡한 통화(ducati|두카트it, soldi|솔디it, pizoli|피졸리it 등)를 사용한 기본 연산, 통화 환전, 이자 계산, 합작 회사의 이익 배분과 같은 주제를 다룬다. 이 책에는 실제로 사용할 수 있는 많은 방법과 규칙(알고리즘)을 강조한 예제들이 가득하다.[17]
제2부는 등차수열, 거듭제곱, 이항 전개, 타르탈리아의 삼각형(파스칼의 삼각형으로도 알려짐), 근을 이용한 계산, 비례/분수를 포함한 일반적인 산술 문제를 다룬다.[18]
제4부는 삼각형, 정다각형, 플라톤 입체, 원의 구적법과 구에 원기둥을 외접하는 것과 같은 아르키메데스의 주제를 다룬다.[19]
2. 3. 탄도학 연구
타르탈리아는 탄도학 연구에 있어서 선구적인 업적을 남겼다. 그의 저서 《노바 시엔티아(Nova scientia)》(1537)는 르네상스 시대 역학에 관한 가장 기본적인 저술 중 하나로 평가받는다.[7] 당시 주류였던 아리스토텔레스 물리학은 운동을 설명할 때 "무거운", "자연적인", "폭력적인"과 같은 범주를 사용하고 수학적 설명을 피했지만, 타르탈리아는 수학적 모델을 적극적으로 도입하여 포물선 운동에 대한 아리스토텔레스의 용어를 제거했다.[8]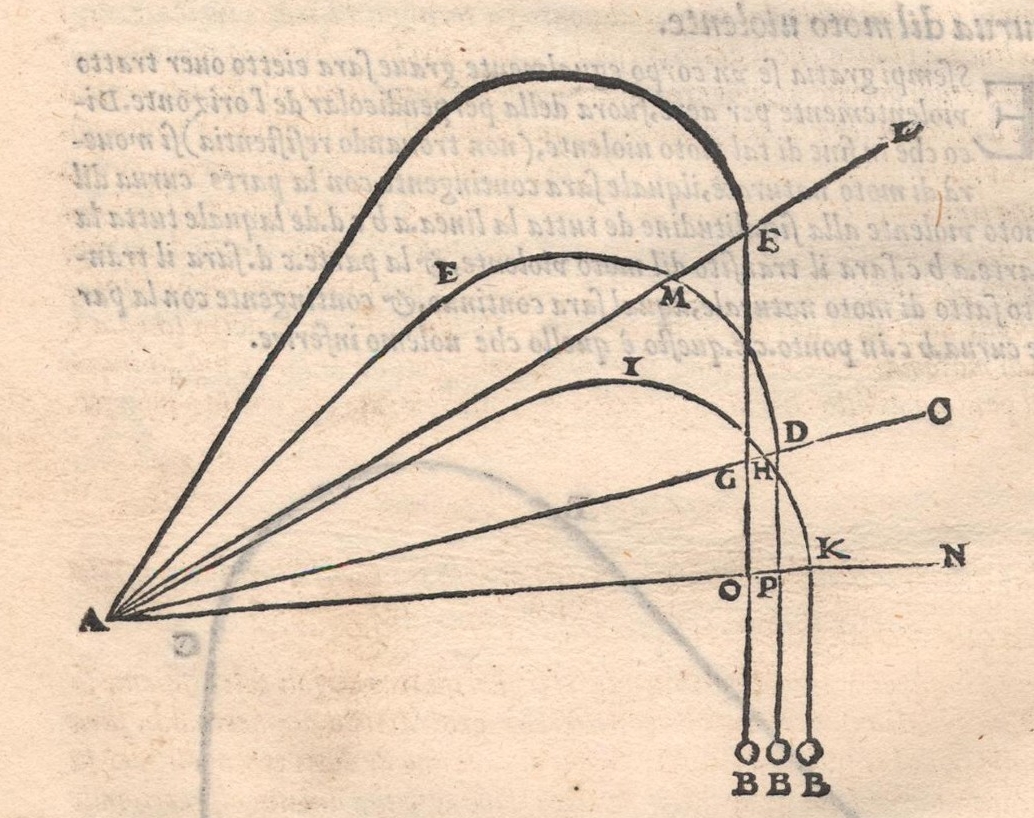
타르탈리아는 발사체의 최대 사거리가 포를 수평선과 45° 각도로 발사했을 때 얻어진다는 것을 발견했다.[9] 그가 제시한 포탄의 비행 모델은 포에서 직선으로 나아가다가 얼마 후 원호를 그리며 지구 쪽으로 휘어지고, 마지막에는 지구를 향해 직선으로 떨어진다는 것이었다.[9] 《노바 시엔티아》 제2권 말미에서 타르탈리아는 45° 각도로 발사된 발사체의 초기 직선 경로 길이를 구하는 방법을 대수적으로 제시했다.[10]
타르탈리아의 군사 과학 저술은 유럽 전역에 큰 영향을 미쳤으며, 18세기까지 포병들의 참고 자료로 활용되었다.[11] 갈릴레오 갈릴레이 역시 타르탈리아의 저술에 큰 영향을 받았으며, 발사체 문제 해결에 있어 그의 연구를 참고했다.[11]
2. 4. 번역
타르탈리아는 고대 그리스 수학자들의 저술을 번역하는 데에도 중요한 역할을 했다. 1543년에 아르키메데스의 저술 중 일부를 라틴어판으로 출판했는데, 여기에는 포물선, 원, 무게중심, 부력에 관한 내용이 담겨 있었다. 1503년에 구아리코(Guarico)가 처음 두 가지에 대한 라틴어판을 출판했지만, 무게중심과 부력에 관한 저술은 그 전까지 출판된 적이 없었다.[13] 이후 타르탈리아는 이탈리아어판도 출판하여, 그의 번역은 고대 그리스 수학 지식을 르네상스 시대 유럽에 널리 알리는 데 기여했다.[13]
1543년 타르탈리아는 원론을 이탈리아어로 번역하여 출판했다. 유클리드의 ''원론''이 현대 유럽 언어로 번역된 것은 이것이 처음이었다.[14] 2세기 동안 유클리드는 아랍어 자료에서 가져온 두 개의 라틴어 번역본을 통해 가르쳐졌는데, 이 번역본에는 비례에 대한 에우독소스 이론인 5권에 오류가 있었다. 타르탈리아의 판본은 손상되지 않은 그리스어 본문의 잠베르티(Zamberti)의 라틴어 번역을 기반으로 하였고, 5권을 정확하게 번역했다. 그는 또한 이 이론에 대한 최초의 현대적이고 유용한 주석을 저술했다.[14] 이 번역본은 갈릴레오에게도 큰 영향을 주었다.[14]
3. 3차 방정식 해법 논쟁
카르다노는 미발표 논문이 타르탈리아의 논문보다 이전에 작성된 것이었기 때문에 자신의 약속을 어겨도 된다고 판단하여, 1545년 자신의 저서 『위대한 기술(Ars Magna)』에 3차 방정식의 해법을 발표했다. 카르다노는 페로와 타르탈리아의 발견임을 명시했지만, 타르탈리아는 카르다노가 약속을 어겼다고 비난하며 공개적인 논쟁을 제안했다. 카르다노는 이를 거부하고 그의 제자 루도비코 페라리가 타르탈리아와 논쟁을 벌였다. 승패에 대해서는 여러 설이 있으며, 페라리가 대승했다는 설이나 페라리의 지각으로 무효 경기가 되었다는 설 등이 있다.[24] 현재 3차 방정식의 해법은 "카르다노-타르탈리아 공식"이라고 불린다.
4. 타르탈리아의 공식
:
여기서 는 꼭짓점 와 사이의 거리를 나타낸다.
5. 타르탈리아의 삼각형
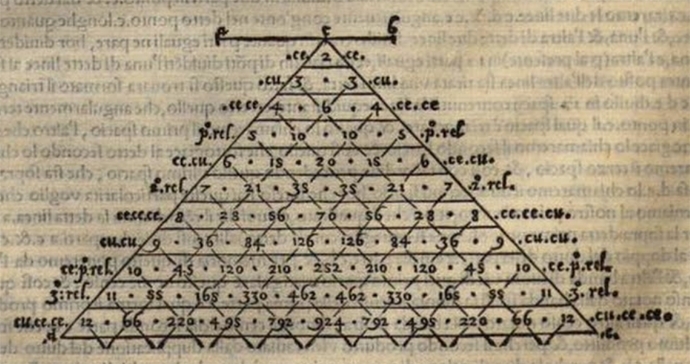
타르탈리아는 이항 전개에 능숙했으며, 그의 저서 『일반 산술 및 측정 논고』(General Trattato) 제2부에는 의 합을 계산하는 방법과 이항 계수를 포함하는 많은 예시가 들어있다.[20] 그는 삼각형 꼭대기에 있는 수평선 가 점 를 꼭짓점으로 하는 두 선분 와 로 나뉘는 방식으로 기하학적으로 생각했다. 이항 전개는 삼각형 아래로 내려갈 때 지수 에 대해 를 취하는 것과 같다. 그는 다섯 번째 줄의 인접한 15와 20을 더하면 여섯 번째 줄에 있는 35가 된다는 덧셈 형성 규칙을 명시적으로 서술했다.[21]
6. 타르탈리아의 문제
이 답은 301 + 420n (n은 0을 포함하는 자연수)이 된다.
7. 저서
참조
[1]
서적
Galileo at Work: His Scientific Biography
Dover
1978
[2]
논문
(제목 없음)
2013
[3]
백과사전
Niccolò Tartaglia
Dictionary of Scientific Biography
[4]
서적
General Trattato di Numeri et Misure, Part IV, Book 3
https://books.google[...]
[5]
논문
Thus Spake al-Khwārizmī: A Translation of the Text of Cambridge University Library Ms. Ii.vi.5
1990
[6]
서적
The Social Origins of Modern Science
[7]
웹사이트
Metallurgy, Ballistics and Epistemic Instruments: The Nova Scientia of Nicolò Tartaglia
http://edition-open-[...]
2013
[8]
논문
How the 'New Science' of Cannons Shook up the Aristotelian Cosmos
2002-07
[9]
웹사이트
Metallurgy, Ballistics and Epistemic Instruments: The Nova Scientia of Nicolò Tartaglia
http://edition-open-[...]
2013
[10]
웹사이트
Metallurgy, Ballistics and Epistemic Instruments: The Nova Scientia of Nicolò Tartaglia
http://www.edition-o[...]
2013
[11]
논문
How the 'New Science' of Cannons Shook up the Aristotelian Cosmos
2002-07
[12]
논문
William of Moerbeke: Translator of Archimedes
[13]
논문
'New Science' of Cannons
[14]
논문
Euclid’s Swan Song: Euclid’s Elements in Early Modern Europe
[15]
문서
1556-1560
[16]
논문
(제목 없음)
1985
[17]
서적
General Trattato di Numeri et Misure, Part I
https://books.google[...]
[18]
서적
General Trattato di Numeri et Misure, Part II
https://books.google[...]
[19]
서적
General Trattato di Numeri et Misure, Part IV
https://books.google[...]
[20]
서적
General Trattato di Numeri et Misure, Part II, Book 2
https://books.google[...]
[21]
서적
General Trattato di Numeri et Misure, Part II, Book 2
https://books.google[...]
[22]
논문
(제목 없음)
1998
[23]
논문
The Cardano-Tartaglia dispute
https://www.jstor.or[...]
1961
[24]
웹사이트
Cardano v Tartaglia: The Great Feud Goes Supernatural
https://arxiv.org/ft[...]
[25]
서적
General Trattato di Numeri et Misure, Part IV, Book 2
https://books.google[...]
[26]
서적
眺めて楽しむ数学 証明の展覧会Ⅱ
東海大学出版会
2003
[27]
서적
新訂 茶の間の数学(上)
聖文新社
2006
본 사이트는 AI가 위키백과와 뉴스 기사,정부 간행물,학술 논문등을 바탕으로 정보를 가공하여 제공하는 백과사전형 서비스입니다.
모든 문서는 AI에 의해 자동 생성되며, CC BY-SA 4.0 라이선스에 따라 이용할 수 있습니다.
하지만, 위키백과나 뉴스 기사 자체에 오류, 부정확한 정보, 또는 가짜 뉴스가 포함될 수 있으며, AI는 이러한 내용을 완벽하게 걸러내지 못할 수 있습니다.
따라서 제공되는 정보에 일부 오류나 편향이 있을 수 있으므로, 중요한 정보는 반드시 다른 출처를 통해 교차 검증하시기 바랍니다.
문의하기 : help@durumis.com